FPGA - Circuits logiques programmables
2023-2025
Cette partie du cours est consacrée aux circuits logiques programmables (FPGA).
Une description HDL (SystemVerilog) peut avoir deux finalités:
La simulation de la logique décrite dans un environnement informatique pour la valider.
La synthèse ou la transformation en un ensemble de ressources physiques pour la mise en œuvre du circuit.
La synthèse est généralement faite automatiquement en utilisant des outils informatiques dédiés (des synthétiseurs) qui vont:
Le résultat de la synthèse peut être, par exemple, une liste de portes logiques et les connexions reliant ces portes. Dans le jargon, ce résultat est appelé netlist (de l’anglais net pour nœud électrique).
La description SystemVerilog peut être utilisée pour deux cibles technologiques:
Le résultat de la synthèse sera une liste de portes logiques qui seront composées de transistors pour fabriquer le circuit. Ceci concerne la fabrication des:
Le résultat de la synthèse sera un fichier binaire pour programmer des circuits contenant de la logique configurable. Ceci concerne principalement les FPGA décrits dans la prochaine section.
Matrice de logique programmable (Field Programmable Gate Array)
Field est à comprendre dans le sens In Field (sur le terrain), en opposition à durant la fabrication.
Un FPGA est donc une matrice de cellules logiques programmables. Dans ce circuit nous pouvons programmer les cellules logiques ainsi que les connexions entre les cellules pour réaliser matériellement des fonctions logiques combinatoires et séquentielles.
Pour différentier la programmation de ces circuits d’un programme logiciel qui s’exécute séquentiellement, on préférera utiliser le terme configurable à la place de programmable.
Un ensemble de ressources configurables:
Pour permettre d’implémenter matériellement toute fonction combinatoire:
Une LUT peut être vue comme une petite mémoire dans laquelle on stocke la table de vérité d’une fonction combinatoire. Chaque bit de la table de vérité est stocké dans un bit de mémoire. Avant de commencer à l’utiliser on charge dans cette mémoire un mot de configuration pour initialiser chaque bit de cette mémoire.
L’adresse de cette mémoire est utilisée comme entrée de la LUT. Comme le montre la figure précédente (ce n’est qu’une figure de principe), changer la valeur de l’entrée (I=\{I_3,I_2,I_1,I_0\}) permet de présenter sur la sortie la valeur d’un bit de configuration différent. La valeur du bit de configuration se propage combinatoirement à travers la logique de décodage de l’adresse (schématisée par l’arbre de multiplexeurs).
Dans l’exemple, nous avons une LUT à 4 entrées. Une table de vérité pour une fonction à 4 entrées contient 16 lignes (2^4), comme le montre la table suivante.
| I | I_3 | I_2 | I_1 | I_0 | O |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | \text{init}_{0} |
| 1 | 0 | 0 | 0 | 1 | \text{init}_{1} |
| 2 | 0 | 0 | 1 | 0 | \text{init}_{2} |
| 3 | 0 | 0 | 1 | 1 | \text{init}_{3} |
| 4 | 0 | 1 | 0 | 0 | \text{init}_{4} |
| 5 | 0 | 1 | 0 | 1 | \text{init}_{5} |
| 6 | 0 | 1 | 1 | 0 | \text{init}_{6} |
| 7 | 0 | 1 | 1 | 1 | \text{init}_{7} |
| 8 | 1 | 0 | 0 | 0 | \text{init}_{8} |
| 9 | 1 | 0 | 0 | 1 | \text{init}_{9} |
| 11 | 1 | 0 | 1 | 0 | \text{init}_{10} |
| 11 | 1 | 0 | 1 | 1 | \text{init}_{11} |
| 12 | 1 | 1 | 0 | 0 | \text{init}_{12} |
| 13 | 1 | 1 | 0 | 1 | \text{init}_{13} |
| 14 | 1 | 1 | 1 | 0 | \text{init}_{14} |
| 15 | 1 | 1 | 1 | 1 | \text{init}_{15} |
Pour configurer notre LUT, il faut donc fournir un mot de configuration init de 16 bits.
Exemples
Si le mot de configuration init = \text{0x8000} (seul init_{15} est à 1) alors la sortie de la LUT est à l’état haut si et seulement si les 4 entrées sont à 1. Nous avons donc le comportement d’une porte ET à 4 entrées.
De façon similaire, si la configuration init = \text{0xFFFE} (seul init_{0} est à 0), alors nous avons les comportements d’un OU à 4 entrées.
Et nous pouvons faire de même avec les 65536 fonctions à 4 entrées possibles.
NOTES Le nombre d’entrées des LUTs des FPGA du commerce peut varier en fonction du fabricant et des modèles.
Chaque cellule logique contient:
La figure précédente représente la structure d’une cellule logique de FPGA avec une LUT à 4 entrées et une bascule D. Un point mémoire de configuration permet de sélectionner comme sortie:
Cette structure de principe se retrouve dans la majorité des FPGA, mais, en fonction des modèles et des choix des fabricants, le nombre et la nature des éléments peut changer. On peut, par exemple, avoir plusieurs sorties configurables, plusieurs LUTs de tailles différentes et plusieurs bascules avec des accès directs. Ceci permet l’implémentation de fonctions plus complexes au sein d’une cellule logique sans passer par les interconnexions externes.
Pour les plus curieux, la structure de la cellule logique du Cyclone V (appelée ALM) est visible sur le site du fabricant. Le Cyclone V est le FPGA que nous utiliserons dans la partie pratique.
Programmer (ou configurer un FPGA) revient à programmer toutes les cellules logiques ainsi que tout le réseau d’interconnexion.
Le fichier de programmation est appelé bitstream
Pour limiter le nombre de signaux nécessaires à la programmation de ces composants, celle-ci se fait généralement par une liaison série interne qui passe par tous les éléments de la matrice.
D’où le terme bitstream (flot d’éléments binaire).
Les points mémoires de configuration des FPGA standards sont réalisés en technologie SRAM. La mémoire SRAM est une mémoire volatile qui perd son contenu si elle n’est pas alimentée. Il faut donc reconfigurer les FPGA à chaque mise sous tension (ou prévoir une mémoire externe non volatile pour reprogrammer le FPGA).
Dans l’ordre des parts de marché
| Fabriquant | Applications |
|---|---|
| AMD/Xilinx | Embarqué, Télécommunication, Data center, … |
| Intel/Altera | Embarqué, Télécommunication, Data center |
| Microchip | Embarqué, Spatial/Avionique/Défense |
| Lattice | Embarqué, Sécurité |
| … |
Les FPGA sont utilisés dans divers domaines allant des systèmes embarqués aux applications de calcul dans les data centers.
Le 1er fabricant de FPGA dans le monde est la société Xilinx (maintenant filiale du fabricant de processeurs AMD). Il est suivi par Altera, une division autonome d’Intel.
Ces deux grands dominent le marché avec plus de la moitié du marché (plus de 60%) et proposent une large gamme de produits allant de petits FPGA low cost pour les systèmes embarqués à de gros FPGA pour les applications de calculs dans les data centers.
À côté de ces deux fabricants, les autres acteurs du marché se sont spécialisés dans niches comme la sécurité, les applications spatiales, l’avionique en proposant des architectures plus spécialisées et/ou des technologies ad hoc.
Il s’agit des différentes étapes par lesquelles on doit passer pour transformer le code HDL (le SystemVerilog) en fichier de programmation pour le FPGA (le bitstream).
On passe généralement par les étapes suivantes:
Ces différentes étapes sont effectuées par des outils logiciels souvent fournis par le fabricant du FPGA. On doit fournir des informations et des contraintes à ces outils, par exemple:

La carte DE1-SoC est une carte fabriquée par Terasic Inc. Elle fait partie de la série des cartes DE développées par Intel/Altera pour son programme académique destiné aux universités et centres de recherche.
C’est pour cette raison que cette carte dispose d’un ensemble d’entrées/sorties, parmi lesquelles:
qui sont très pratiques pour apprendre, mais peut-être moins utiles dans une application industrielle.
- Reprendre le décodeur 7 segments pour la mise en œuvre d’un compteur.
Téléchargez l’archive contenant le projet du TP ici puis décompressez là.
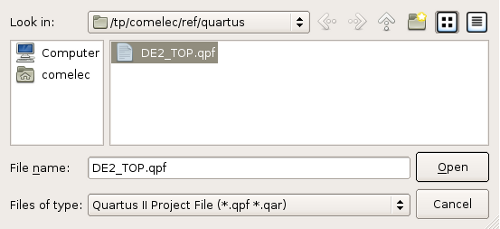
Lancer Quartus (dans le groupe des applications de développement), puis ouvrir le projet:
Le fichier contenant la configuration du projet a l’extension
*.qpf:
module dec7seg(input [3:0] i, output logic[6:0] seg);
always_comb
case(i)
// abc_defg
4'h0: seg = 7'b100_0000;
4'h1: seg = 7'b111_1001;
4'h2: seg = 7'b010_0100;
4'h3: seg = 7'b011_0000;
4'h4: seg = 7'b001_1001;
4'h5: seg = 7'b001_0010;
4'h6: seg = 7'b000_0010;
4'h7: seg = 7'b111_1000;
4'h8: seg = 7'b000_0000;
4'h9: seg = 7'b001_0000;
4'hA: seg = 7'b000_1000;
4'hB: seg = 7'b000_0011;
4'hC: seg = 7'b100_0110;
4'hD: seg = 7'b010_0001;
4'hE: seg = 7'b000_0110;
4'hF: seg = 7'b000_1110;
endcase
endmoduleAu moment de sauvegarder, nommer le fichier
dec7seg.sv et vérifier que le fichier est bien ajouté au
projet.
Modifier ensuite le fichier contenant le module
DE1_SoC.
Nous voulons ajouter un compteur sur 8 bits dont la sortie est affichée sur deux afficheurs 7 segments. Comme l’horloge principale de la carte FPGA a une fréquence de 50 MHz, il faut prévoir un mécanisme pour que le compteur n’évolue pas trop vite. Nous ajoutons donc un second compteur pour générer un signal d’activation à une cadence plus raisonnable.
Le code suivant est une implémentation possible:
// Un compteur pour réduire la vitesse
// Il comptera 25e6 cycles pour avoir deux changements par seconde
// Ici on déclare des constantes
localparam MAX_DIV = 50_000_000/2 - 1;
// la partie entière du Log2
localparam DIV_WIDTH = $clog2(MAX_DIV);
// Le signal du compteur de division de fréquence
logic [DIV_WIDTH-1:0] c_div;
always@(posedge clock_50 or negedge reset_n)
if(!reset_n) begin
c_div <= 0;
end
else begin
if(c_div == MAX_DIV)
c_div <= 0;
else
c_div <= c_div + 1;
end
// Ce signal n'est à 1 que durant un cycle 2x par seconde
logic ena_2hz;
assign ena_2hz = (c_div == MAX_DIV);
// Le compteur 8-bits qui s incrémente 2x par seconde
logic [7:0] counter;
always@(posedge clock_50 or negedge reset_n)
if(!reset_n) begin
counter <= 0;
end
else begin
if(ena_2hz)
counter <= counter + 1 ;
endPuis instancier les décodeurs pour contrôler les afficheurs
hex0 et hex1.
dec7seg dec0(.i(counter[3:0]),.seg(hex0));
dec7seg dec1(.i(counter[7:4]),.seg(hex1));Ne pas oublier de supprimer les lignes où les sorties
hex0 et hex1 sont forcées à
0.
On peut ensuite:
 )
) ) et vérifier que ça fonctionne
) et vérifier que ça fonctionneLa carte DE1-SoC embarque un CODEC audio.
Ce composant contient un convertisseur analogique numérique (ADC) et un convertisseur numérique analogique(DAC). La figure suivante montre ce composant ainsi que les entrées sorties audio qui y sont reliées.
Les signaux audio analogiques provenant des entrées micro (rose) et ligne (bleue) sont convertis en signaux numériques qui sont transmis en série (bit par bit) au FPGA. Réciproquement, le FPGA peut transmettre des signaux numériques au CODEC qui les convertira en un signal analogique sur la sortie ligne (en vert sur la figure).
Une interface supplémentaire, venant du FPGA, permet de paramétrer le CODEC (format des données, fréquence d’échantillonnage…)
Le projet du TP contient les modules nécessaires pour configurer et communiquer avec le CODEC.
La figure suivante montre la structure du projet.
Le CODEC est configuré pour échantillonner les signaux audio à 48 KHz. La communication avec le CODEC utilise une horloge de 12 MHZ et nous avons inclus des modules permettant la déserialisation des données entrantes (venant de l’ADC) et la sérialisation des données sortante (allant vers le DAC).
Pour implémenter les fonctions de traitement du signal vous n’avez à
modifier que le module audio_proc. Au niveau de ce module,
vous recevez les signaux suivant:
| signal | direction | taille | fonction |
|---|---|---|---|
clk |
entrée | 1 bit | horloge à 12MHz |
reset_n |
entrée | 1 bit | signal de remise à 0 actif sur niveau bas |
audio_data_enable |
entrée | 1 bit | indique l’arrivée d’un nouvel échantillon |
adc_data_x |
entrée | 16 bit | les échantillons venant de l’ADC (canal gauche et droit) |
dac_data_x |
sortie | 16 bit | les échantillons allant vers le DAC (canal gauche et droit) |
Tous les 20.83\mu\text{s} (1/48\text{KHz}), le signal
audio_data_enable passe à 1 durant un cycle d’horloge pour
signaler l’arrivée d’un nouvel échantillon sur les entrées
ad_adc_data_x. Simultanément, les sorties
dac_data_x sont capturées pour être envoyées vars le
convertisseur numérique analogique (DAC).
Une modulation par une porteuse sinusoïdale de fréquence bien choisie:
S_i(t) = S(t) \cdot \cos(2\pi f_0 t)
suivie d’un filtre passe bas.
Ou en temps discret:
S_i(n) = S(n) \cdot \cos(2\pi \frac{f_0}{f_s} n)
Où f_s est la fréquence d’échantillonnage.
Vous pouvez trouver ici un fichier dans lequel le signal audio a subi cette transformation, avec les paramètres suivant:
Cette transformation est réversible en la réappliquant!
Mise en œuvre de la modulation
Calculez les valeurs successives de quelques échantillons du signal S_i en fonction du signal d’entrée S.
Proposez un opérateur séquentiel pour mettre en œuvre cette fonction.
Écrivez le code SystemVerilog pour cet opérateur.
Testez!
Normalement, à la fin de l’étape précédente, vous devriez entendre correctement le son d’origine sans besoin de filtre supplémentaire. En effet, la qualité du chemin audio (les casques et vos oreilles) fait qu’il est difficile d’entendre les fréquences élevées. Il y a un filtre “naturel”.
Pour permettre malgré tout de mettre en œuvre le filtre (et entendre quelque chose), nous vous proposons ici un second fichier audio avec un bruit haute fréquence, artificiellement ajouté.
L’équation du filtre à implémenter est la suivante:
S_f(n) = \sum_{i=0}^7 c_i \cdot Si(n-i) où les c_i sont les 8 coefficients du filtre.
| index | value |
|---|---|
| 0 | -0.075163 |
| 1 | 0.024881 |
| 2 | 0.150253 |
| 3 | 0.288582 |
| 4 | 0.348980 |
| 5 | 0.288582 |
| 6 | 0.150253 |
| 7 | 0.024881 |
Ces paramètres ont été obtenus en utilisant un outil de synthèse de filtres numériques. Nous avons limité le nombre de coefficients à 8 et ciblé une fréquence de coupure à 10 KHz.
La qualité du filtrage obtenue n’est pas excellente, mais juste suffisante pour faire le TP.
Mise en œuvre du filtrage
Comment représenter les coefficients du filtre pour construire cet opérateur?
Comment conserver les 8 derniers échantillons?
Proposez un opérateur séquentiel pour mettre en œuvre cette fonction.
Écrivez le code SystemVerilog pour cet opérateur.
Testez!
Les échantillons venant du CODEC sont signés (en Complément à 2), ceci doit être pris en compte dans la déclaration des signaux permettant de les manipuler.
Par défaut, les vecteurs de bits déclaré comme
logic[i:0] sont considérés comme des nombres non signés.
Les opérations arithmétiques ainsi que les opérations de comparaison
arithmétique les interpréteront donc comme des nombres non signés.
Pour pouvoir faire de l’arithmétique sur des nombres signés il faut
utiliser le mot clé signed au moment de la déclaration.
// deux signaux de 4 bits transportant une valeur signée
logic signed [3:0] s_0, s_1;
assign s_0 = 4'b1111; // -1 en CA2
assign s_1 = 4'b0111; // +7 en CA2
... if(s_0 > s_1)... // faux car -1<+7
logic signed [15:0] r_0, r_1;
assign s_0 = -1; // ou 16'hff_ff
assign s_1 = +1; // ou 16'h00_01ATTENTION pour que le résultat signé d’une opération arithmétique soit correct, il faut que tous les opérandes soient déclarés comme signés.
| © Copyright 2022-2025, Télécom Paris. | |

|
Le contenu de cette page est mis à disposition selon les termes de la licence Creative Commons Attribution - Partage dans les Mêmes Conditions 4.0 International. |