Cette partie du cours est consacrée à la logique combinatoire. Nous allons aborder deux aspects:

1. la construction de portes combinatoire en utilisant des transistors MOS: les portes CMOS
2. la description du comportement de ces portes dans un langage de description du matériel (SystemVerilog)

Dans cette première section nous nous intéressons à la construction de portes en logique MOS complémentaire (CMOS). Nous commençons par reprendre l’inverseur, vu dans le cours d’introduction, puis nous présenterons quelques exemples de portes plus complexes. Nous finirons la section par une analyse des performances (la vitesse et la consommation énergétique) de ces portes.

Les transistors MOS peuvent être utilisés comme interrupteurs commandés. Ce modèle n’est valable que si les transistors sont correctement polarisés.

Ainsi, il faut que:

• la source du nMOS soit à une tension plus basse que la grille (V_{ss}),
• la source du pMOS soit à une tension plus haute que la grille (V_{dd}).

Si ces conditions ne sont pas respectées, le modèle d’interrupteur n’est plus valide.

Pour cela, dans la suite,

• les transistors nMOS apparaitront toujours du côté bas des schémas et
• les transistors pMOS apparaitront toujours du côté haut.

Si ces conditions sont respectées, on peut voir les transistors comme des interrupteurs commandés qui par la tension de la grille comme résumé dans les tables suivantes.

• Pour les nMOS:

• Pour les pMOS:

Comme nous manipulons des signaux transportant une information binaire, les tensions qui nous intéressent sont celles qui correspondent à la grille reliée à la masse ou reliée à l’alimentation.

• Pour le nMOS (la source reliée à la masse):

• Pour le pMOS (la source reliée à l’alimentation):

Cette porte est la porte CMOS la plus simple que nous pouvons construire. Elle est composée de deux transistors:

• Un nMOS avec sa source connectée à la tension la plus basse du circuit V_{ss}.
• Un pMOS avec sa source connectée à la tension la plus haute du circuit V_{ds}.

NOTE V_{ss} est généralement la référence de tension du circuit (la masse, gnd).

Examinons le comportement de cette porte quand l’entrée change.

• i est à l’état logique 1

La tension V_i est égale à V_{dd}. C’est la tension appliquée aux grilles des deux transistors.

Comme cette tension est plus grande que la tension de seuil V_T du transistor nMOS celui-ci est passant. La tension entre le drain et la source du transistor nMOS est porche de 0 et la sortie o est ainsi connectée à la tension la plus basse du circuit.

Du côté du transistor pMOS, V_{gs} = 0V. En valeur absolue, elle est inférieure à la tension de seuil du transistor pMOS (|V_{gs}|<V_T) ce qui fait que ce transistor est bloqué.

Un transistor bloqué peut être vu comme un circuit ouvert. Il n’y a donc pas de liaison entre la sortie o et la tension haute v_{dd} du circuit.

La tension sur la sortie est donc égale à V_{ss} ce qui correspond à un niveau logique 0.

• i est à l’état logique 0

La tension V_i est cette fois-ci égale à V_{ss}.

Du côté du transistor nMOS, V_{gs} = 0V < V_{T}, le transistor est bloqué. Alors que du côté du transistor pMOS, |V_{gs} - V_{dd}| > V_{T} et donc ce transistor est passant.

Nous avons donc la sortie o qui est connectée à la tension la plus haute du circuit V_{dd} et donc un état logique haut.

La table suivante résume les deux états:

Et si on ne garde que les états logiques:

Ce qui est bien la table de vérité d’un inverseur logique (o = \overline{i}).

L’intérêt principal de cette structure, est que dans aucun des deux cas, il n’existe un chemin de conduction qui relirait l’alimentation (V_{dd}) à la masse (V_{ss}). Il n’y a donc pas de consommation électrique (au-delà de fuites liées à l’imperfection de l’état bloqué des transistors) si l’état des entrées ne change pas.

Dans la suite, pour simplifier les raisonnements, nous ne considèrerons les transistors comme des interrupteurs commandés avec le comportement suivant:

• un transistor nMOS est un interrupteur:
  • ouvert si sa grille est à l’état logique bas (0)
  • fermé si sa grille est à l’état logique haut (1)
• un transistor pMOS est un interrupteur:
  • fermé si sa grille est à l’état logique bas (0)
  • ouvert si sa grille est à l’état logique haut (1)

Il faudra garder à l’esprit que ceci est valide tant que les niveaux de tension électriques sont corrects par rapport aux seuils des transistors.

Dans l’équation précédente, \sum et \prod font référence aux opérateurs booléens (le OU et ET).

Le réseau N, quand il est passant, ne peut que mettre à 0 la sortie, alors que le réseau P ne peut que la mettre à 1. Il faudra s’assurer que les deux réseaux ne sont pas passants simultanément.

Cette généralisation a ses limites, car:

1. toutes les fonctions booléennes ne peuvent s’exprimer sous cette forme,
2. et, que la taille des réseaux est limitée par le nombre de transistors que l’on peut avoir en série.

Concernant ce dernier point, quand le nombre de transistors en série (dans le réseau N ou P) augmente, on éloigne ces derniers du potentiel des lignes d’alimentations et les transistors ne se comportent plus comme des interrupteurs. Ceci limite donc le nombre d’entrées que nous pouvons avoir dans une porte CMOS, typiquement à 3 ou 4 entrées maximum.

Ces limites ne sont pas vraiment un problème. Les fonctions logiques sont décomposées en fonctions plus simples, pour lesquelles on peut construire des portes CMOS, qui sont ensuite connectées entre elles.

Dans la suite, quelques exemples de construction de portes CMOS habituelles.

En parant de l’équation logique de la porte, on peut exprimer:

1. le complément de la sortie en fonction des entrées. Ceci représente les états des entrées pour lesquels la sortie passe à 0. On peut ainsi déduire la structure du réseau N.

Pour la porte NAND, la sortie est à 0 si et seulement si les deux entrées sont à l’état haut.

Ce qui revient à dire que la sortie est connectée à la masse seulement si les deux transistors N commandés par les entrées a et b sont passant. D’où la structure du réseau avec les deux transistors en série.

2. la sortie en fonction du complément des entrées. Ceci représente les états des entrées pour lesquels la sortie passe à 1.

Pour la porte NAND, la sortie est à 1 si une des deux entrées sont à l’état bas. Ce qui revient à dire que la sortie est connectée à l’alimentation si un des transistors P commandés par les entrées a et b est passant. D’où la structure du réseau avec les deux transistors en parallèle.

La table suivante résume ce raisonnement:

Notez que d’un point de vue structurel, des transistors disposés en série correspondent à un ET alors que quand ils sont disposés en parallèle, ceci correspond à un OU.

Avec le même raisonnement que pour la porte NAND, on obtient une structure duale.

Ici aussi la sortie est inversée et ne dépend que des entrées non inversées. Nous voyons que nous pouvons construire ce type de portes en suivant la même méthodologie.

Si l’équation de la porte n’est pas directement exprimable comme le complément de la somme ou du produit de ses entrées, il faut la décomposer.

Assez simple ici d’exprimer la fonction logique de la porte comme l’inverse d’une porte simple. Parfois c’est un peu plus complexe comme le montre l’exemple suivant.

Pour ce type de portes, on a pas le choix, il faut avoir en même temps, les entrées et leur complément.

Il faut pour cela ajouter deux inverseurs qui génèrent les signaux complémentaires. Les sorties de ces portes seront connectées à des signaux internes à la porte.

Pour la porte XOR, dans la figure, nous avons deux inverseurs dont les sorties son na et nb.

\begin{aligned} na & = \overline{a}\\ nb & = \overline{b} \end{aligned}

On peut donc réécrire les équations de la sortie et de la sortie complémentaire comme:

\begin{aligned} o & = a \cdot nb + na \cdot b\\ \overline{o} & = na \cdot nb + a \cdot b \end{aligned}

et en déduire les réseaux N et P correspondant.

Les grilles (entrées des portes CMOS) ne laisse pas passer de courant en régime permanent. Par contre, elles se comportent comme des condensateurs et en régime transitoire, il faut les charger ou décharger pour changer leur état. De plus, les connexions métalliques reliant les portes vont ajouter des capacités parasites.

Pour simplifier le problème, nous pouvons représenter l’ensemble de ces capacités par une capacité équivalente en sortie de la porte. Cette capacité équivalente peut être décomposée en deux parties:

C_L = C_i + C_e

• C_i intrinsèque à la porte,
• C_e extrinsèque, liée aux éléments connectés à la porte.

On s’intéressera dans la suite à la décharge de la capacité à travers les transistors nMOS.

• l’entrée passe de 0 à 1 (de 0 V à V_{dd})
• la sortie passe de 1 à 0 (de V_{dd} à 0 V)

Le cas dual est similaire en considérant le transistor pMOS.

1. Initialement la sortie de la porte est à V_{dd} et le transistor nMOS est bloqué
   • sa tension de grille V_{GS} est à 0 V
   • la tension entre drain et source V_{DS} est à V_{dd}
   • le courant qui le traverse est nul (I_{DS}=0)
2. Le transistor nMOS devient passant
   • sa tension de grille V_{GS} passe à V_{dd}
   • la sortie est toujours à V_{dd}
   • Le courant qui traverse le transitor est le courant de saturation (I_{DS max})
3. Le courant de décharge est maintenu constant par le transistor
   • la sortie se décharge à courant constant
4. Jusqu’à ce que la tension en sortie de la porte passe sous le seuil de basculement logique
   • V_{dd}/2 dans le schéma

Le courant de décharge est imposé par le transistor nMOS. Comme la tension à l’entrée de la grille est égale à V_{dd}, ce courant est initialement égal au courant de saturation I_{DS max}.

La valeur de ce courant est liée à la tension d’alimentation et à la physique et dimensions du transistor.

I_{DSmax} = K_n \cdot (V_{dd} - V_t)^2

avec,

K_n = \frac{1}{2} \mu_{0N} \cdot C'_{ox} \frac{W_N}{L_N}

• W_N, L_N sont respectivement la largeur et longueur du transistor,
• C'_{ox} la capacité de la grille par unité de surface,
• et \mu_{0N} la mobilité (lié à la qualité des semi-conducteurs)

Ce qui permet d’exprimer le temps de propagation (avoir un modèle)

t_p = C_L \frac{\Delta V}{I_{DSmax}} = C_L \frac{\frac{V_{dd}}{2}}{K_n\cdot(V_{dd}-V_t)^2}

On peut décomposer ce temps en deux parties:

• intrinsèque à la porte t_{p0},
• extrinsèque, dépendant de la charge.

t_p = t_{p0} + d_{tp} \cdot C_e

avec,

• t_{p0} = d_{tp}\cdot C_i
• d_{tp} = \frac{V_{dd}}{2K_n(V_{dd}-V_t)^2} (dépendance capacitive)

Considérons la charge à travers le transistor pMOS.

Au niveau de l’alimentation:

• la tension est constante v_{pwr} = V_{dd}
• le courant est celui qui charge la capacité i_{pwr} = i_{c}

L’énergie fournie:

\begin{aligned} E_{pwr} & = \int_0^{\infty} V_{dd} ( C_L \frac{\text{d} v_c}{\text{d}t}) \text{d}t\\ & = \int_0^{V_{dd}} V_{dd} \cdot C_L \cdot \text{d} v_c\\ & = C_L \cdot V_{dd}^2 \end{aligned}

An niveau de la capacité:

• la tension v_c évolue de 0 à V_{dd},
• le courant est le même i_c = C_L \frac{\text{d} v_c}{\text{d}t}

L’énergie emmagasinée dans la capacité:

\begin{aligned} E_{c} & = \int_0^{\infty} v_{c} ( C_L \frac{\text{d} v_c}{\text{d}t}) \text{d}t\\ & = \int_0^{V_{dd}} v_{c} \cdot C_L \cdot \text{d} v_c\\ & = \frac{1}{2} \cdot C_L \cdot V_{dd}^2 \end{aligned}

La moitié de l’énergie fournie par l’alimentation a été dissipée par effet joule dans les transistors.

Pour un circuit complexe,

• fonctionnant à la fréquence f,
• avec un taux d’activité \alpha (la proportion de portes qui changent d’état à chaque cycle),

la puissance consommée est de la forme:

P \propto \alpha f C_L V_{dd}^2

On voit que cette puissance est proportionnelle à la fréquence de fonctionnement, et au carré de la tension d’alimentation. La capacité est quant à elle liée à la technologie et taille des transistors.

Voici deux exemples montrant les informations qui sont fournies avec une bibliothèque de cellules précarctérisées.

Ces exemples sont extraits de la documentation de la bibliothèque NanGate/Silvaco OpenCell 45nm Library.

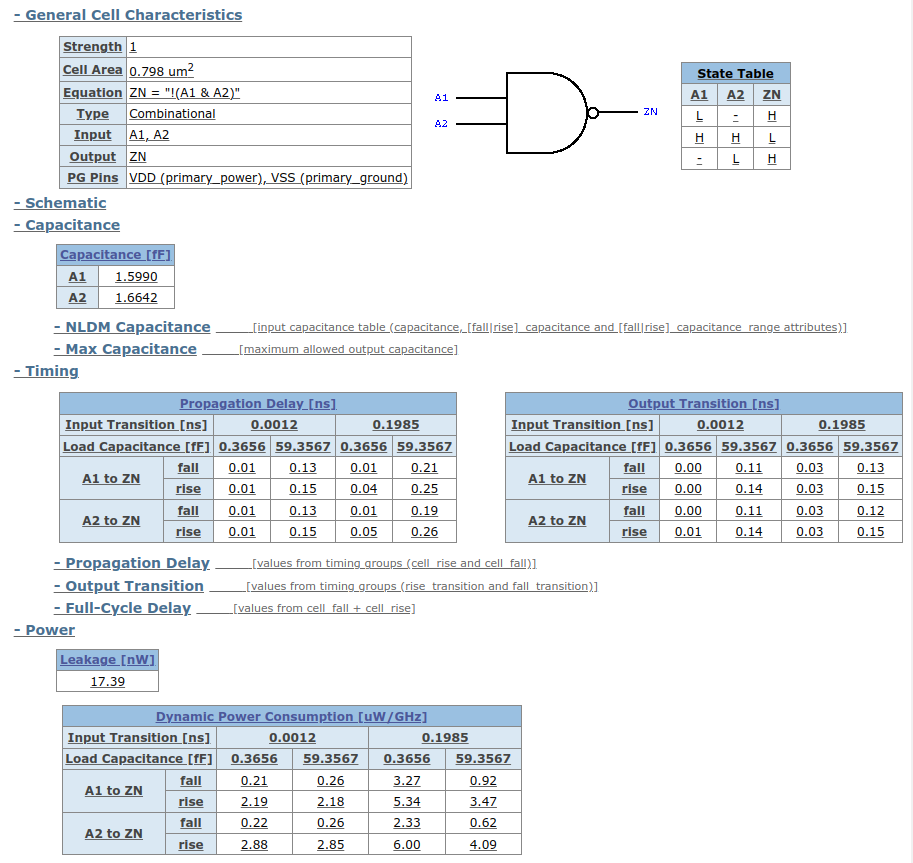
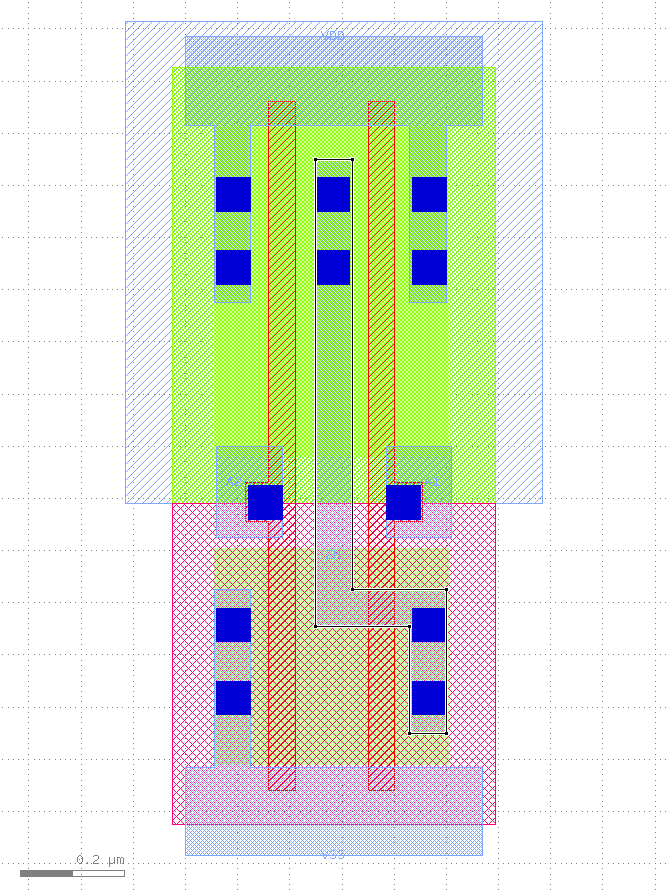
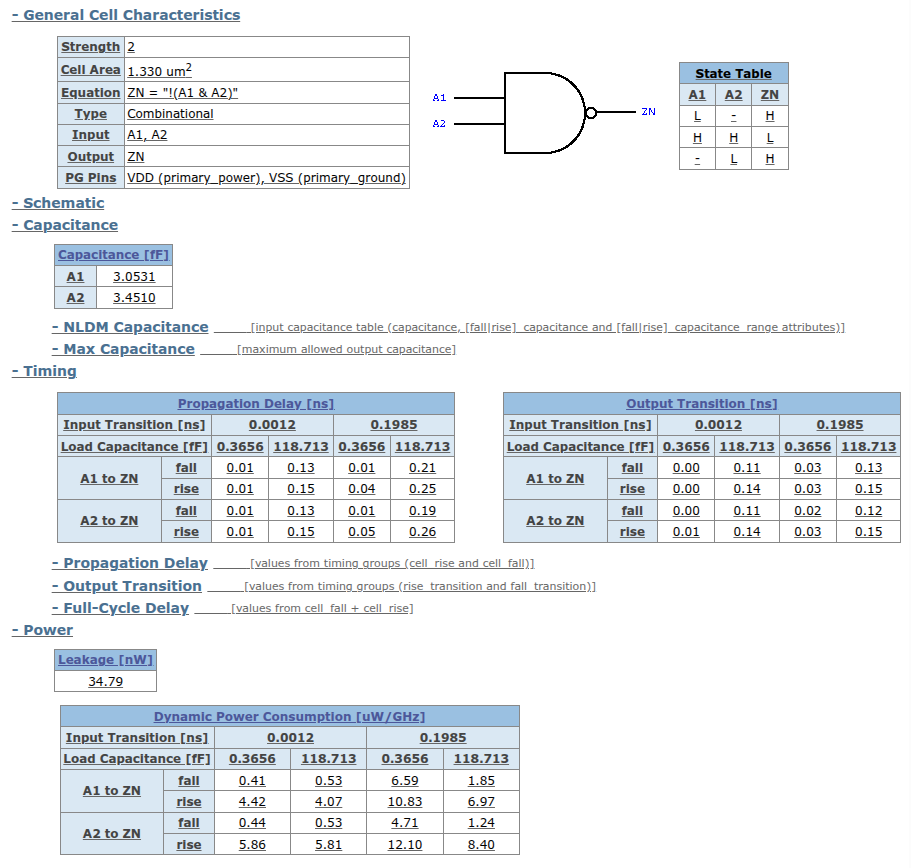
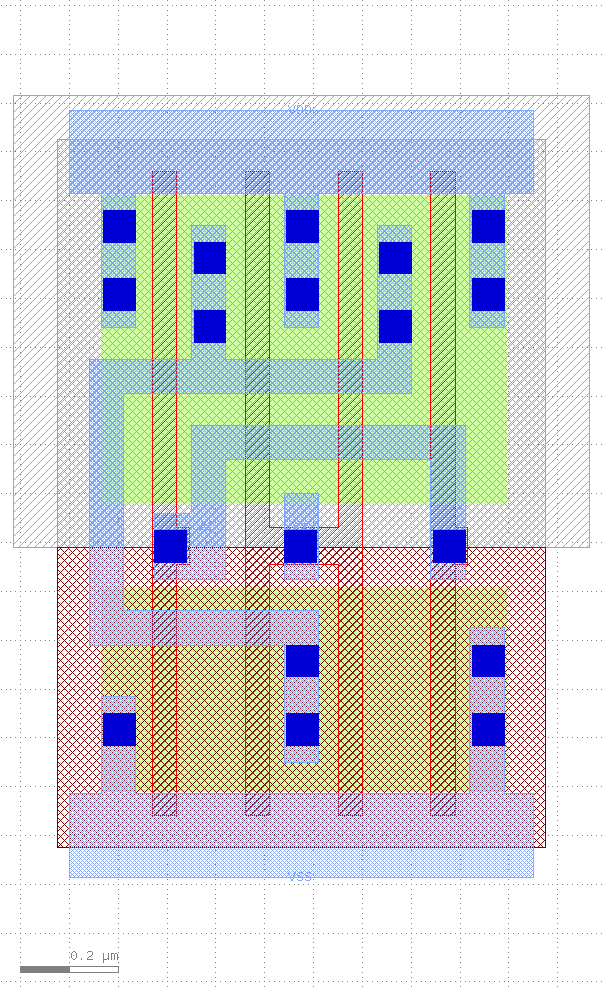
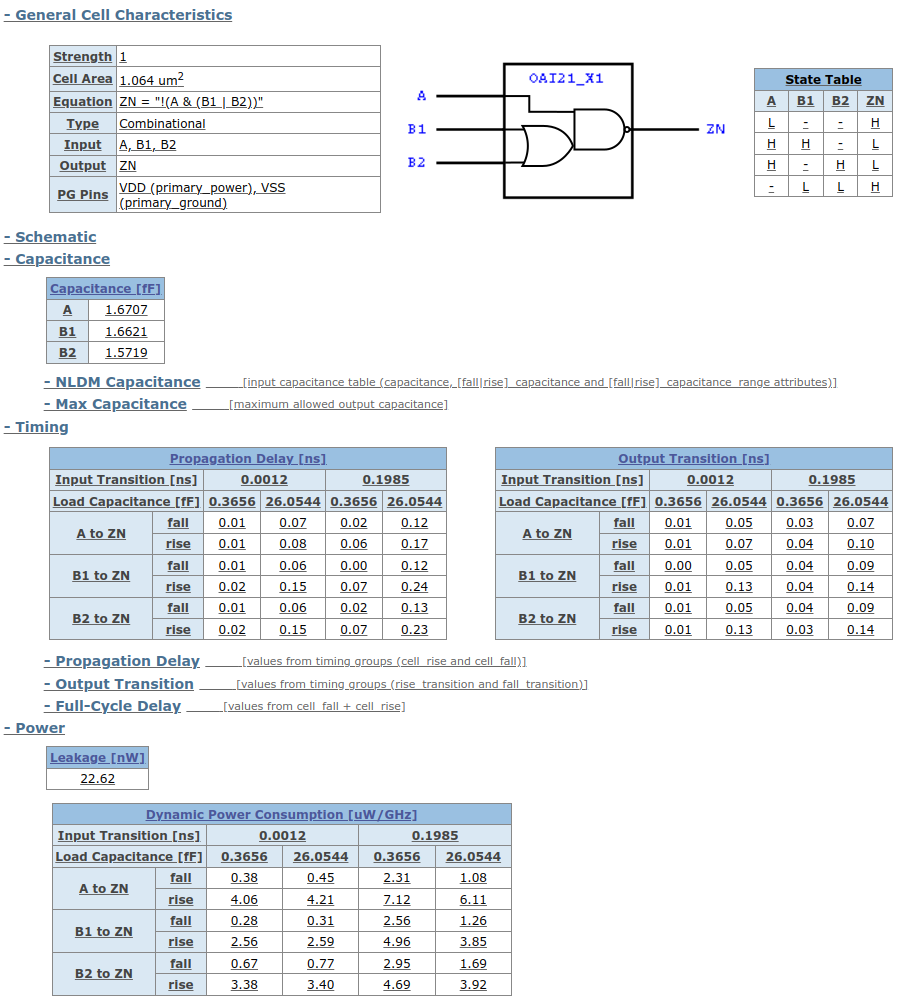
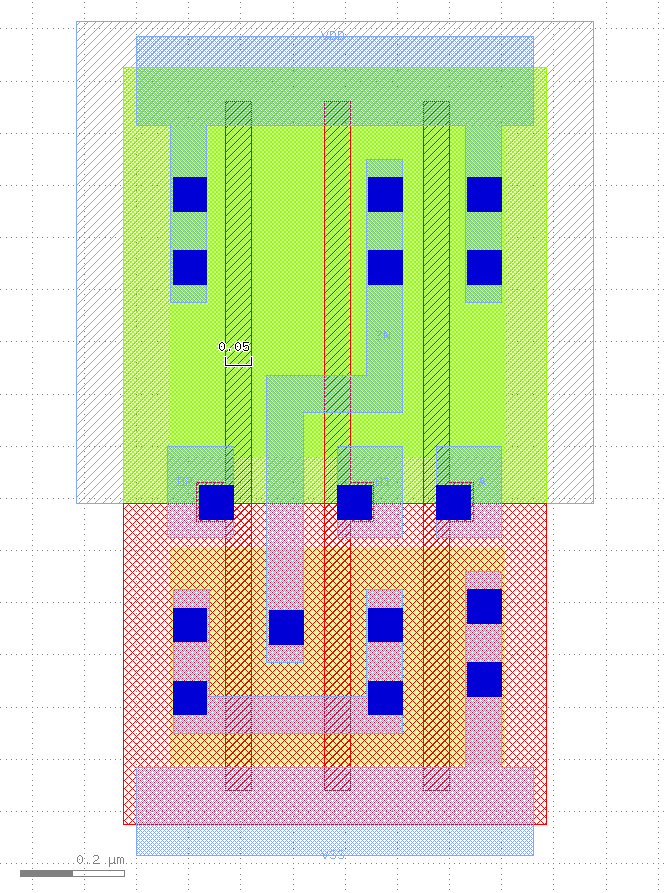
Pour chaque porte, nous aurons au moins des informations concernant:

• les capacités de chaque entrée,
• les temps de propagation à vide et la dépendance capacitive,
• la consommation liée aux changements des états.

Ces informations sont fournies sous forme de fichiers informatiques qui seront utilisés par des outils informatiques pour automatiser la conception des circuits logiques.

On parle d’EDA pour Electronic Design Automation. Ces outils vont piocher dans les bibliothèques précaractérisée pour transformer des représentations abstraites en assemblage de portes puis de transistors.

Ces outils permettent:

• synthétiser : transformer la représentation abstraite en portes,
• placer et router : choisir les portes et les connecter entre elles,
• analyser les performances : estimer les temps de propagation et la consommation.

Un langage de description du matériel (HDL pour Hardware Description Language) est un langage informatique qui sert à décrire la structure et le comportement de blocs électroniques numérique.

Ces langages permettent d’utiliser des outils informatiques pour simuler, analyser et concevoir des blocs matériels numériques.

Ils sont différents d’un langage de programmation dans le fait qu’ils ont comme objectif de concevoir des composants matériels, alors qu’un langage de programmation standard a pour objectif de produire une séquence d’instruction qui sera exécutée par un processeur.

Dans l’industrie, deux familles de langages existent, Verilog/SystemVerilog et VHDL. Bien que les syntaxes soient différentes, les concepts manipulés et les objectifs sont quasi identiques.

Dans ce cours, nous allons vous présenter quelques bases de SystemVerilog pour représenter de la logique combinatoire, puis de la logique séquentielle.

Les modules sont déclarés avec le mot-clé module (mot réservé). Ce module doit avoir un nom (foo dans l’exemple).

• les entrées sont déclarées avec le mot-clé input.
• les sorties sont déclarées avec le mot-clé output.

Dans l’exemple, les entrées et sorties sont de type logic. Cela signifie qu’elles correspondent à des entrées/sorties logiques sur 1 bit.

NOTE Tout code SystemVerilog doit appartenir à un module!

Pour des bus sur plus d’un bit, il faut utiliser des crochets [...] pour préciser la taille (plus précisément, on précise les indices de début et de fin du bus).

Par exemple:

input logic [3:0] A

A est un bus en entrée du module, composé des quatre bits suivant: a[3],a[2],a[1] et a[0]. a[3] étant le bit de poids fort (msb pour most significant bit ), et a[0] le poids faible (lsb pour least significant bit).

La valeur transportée par ce bus est par défaut celle d’un nombre entier non signé.

A = \sum_0^3 a[i] \cdot 2^i

Le mot clé assign permet d’exprimer le fait que nous avons une affectation continue (continuous assignment).

Contrairement à un langage de programmation standard, ici nous exprimons le fait que le signal logique à gauche de l’affectation (à gauche du =) est continument connecté à la sortie d’une porte logique dont l’équation booléenne est donnée à droite de l’affectation.

La syntaxe de SystemVerilog est héritée de celle du langage C, les symboles utilisés pour les différents opérateurs sont très similaires.

Au-delà de la logique booléenne pure, il est possible d’utiliser d’autres opérateurs pour des fonctions combinatoires plus complexes.

NOTE Pour les signaux binaires, les opérateurs logiques et les opérateurs bit-à-bit sont équivalents.

DigitalJS est un outil libre, en ligne, permettant d’analyser et simuler du code SystemVerilog. Il fait appel à plusieurs outils libres:

• Yosys un outil de synthèse libre pour transfromer le code en ensemble de blocs/portes électronique,
• Verlator un second outil libre utilisé ici pour du Lint (analyse de code).

Le résultat peut être simulé dans son navidateur web en utilisant les ressources locales de sa machine.

DigitalJS a été conçu pour une utilisation dans le cadre d’activités pédagogique. Bien qu’il ne soit pas parfait (et ne supporte pas l’entièreté de SystemVerilog), il est suffisamment performant pour être utilisé dans le contexte su cours. Il est ainsi possible de faire des démonstrations et des travaux pratiques sans installer le moindre outil sur sa machine.

La figure suivante montre un exemple de l’interface de l’outil:

Pour démarrer, il suffit:

• de créer un fichier
  • ou de charger des fichiers locaux
• d’écrire son code SystemVerilog
  • le code peut être téléchargé pour le sauvegarder (notez l’icône avec la flèche dans l’onglet d’édition)
• lancer l’outil en appuyant sur le bouton Run
  • si le code est correct, le résultat apparait sur le panneau de droite

Une fois lancé ou peut interagir avec le résultat en agissant sur les entrées du module. Pour les entrées binaires, l’outil affiche des boutons cliquables. Les sorties sont représentées par des leds rouges quand elles sont à 0 et vertes quand elles sont à 1.

Les entrées/sorties sur plus d’un bit sont représentées par leur valeur numérique (en hexadécimal par défaut, mais on peut changer la représentation).

Le but ici est de:

• écrire un premier module SystemVerilog décrivant de la logique combinatoire
  • utiliser les opérateurs logiques
  • utiliser les affectations continues
• apprendre comment on peut réutiliser un module pour décrire structurellement un opérateur plus complexe.

Note pour plus tard Ceci est un exercice destiné à vous familiariser avec la syntaxe et les concepts du langage. Les opérateurs arithmétiques existent en SystemVerilog et au-delà de cet exercice, il sera préférable de décrire les additionneurs en utilisant l’opérateur prévu pour cela.

Un additionneur 1 bit complet possède 3 entrées:

• les deux bit qu’on doit sommer,
• un entrée de retenue venant d’une opération précédente.

Il possède deux sorties la somme et une retenue.

Pour le décrire, nous devons déclarer un module (ici nommé FA) avec l’interface suivante:

• trois entrées logiques sur 1 bit a, b et ci (input carry),
• deux sorties logiques sur 1 bit s et co (output carry).

Nous vous rappelons que:

• la somme sur 1 bit est obtenue en faisant le ou-exclusif des entrées,
• la retenue, quant à elle, correspond à la sortie de la porte majorité (deux entrées parmi trois à 1).

D’où le code SystemVerilog donné.

Travail à faire

Reprenez ce code dans DigitalJS et assurez-vous que le comportement obtenu est correct (par exemple et reconstituant la table de vérité).

Nous avons besoin ici d’un complément sur la syntaxe de SystemVerilog pour pouvoir décrire la structure d’un opérateur complexe en réutilisant des modules existants.

SystemVerilog permet de créer des instances d’un module existants.

Sous-modules et instances de modules

Considérons l’exemple suivant avec un module X:

module X (input logic a, output logic b);
//...
endmodule

Si nous voulons utiliser le module X à l’intérieur d’un autre module Y, il faut l’instancier.

module Y(input logic i, output logic o);

   // instance of module X
   X X_0(.a(i), .b(o));

endmodule

Dans cet exemple nous avons créé une instance X_0 du module X. Nous avons connecté:

• l’entrée a de X_0 au signal i de Y,
• la sortie b de X_0 au signal o de Y.

Ceci est appelé une description structurelle de Y.

Signaux internes

Dans l’exemple précédent, les entrées/sorties du sous-module sont connectées directement aux entrées/sortie du module de niveau supérieur.

Si nécessaire, il est possible de déclarer des signaux internes au module de niveau supérieur.

Dans l’exemple suivant, le module Y contient deux instances du module X (X_0 en X_1). Ces deux instances sont connectées en interne du module Y par le signal logic s.

module Y(input logic i, output logic o);

 logic s;

 X X_0(.a(i), .b(s));
 X X_1(.a(s), .b(o));

endmodule

s n’apparait pas dans l’interface de Y, il est interne.

La sortie b de X_0 est connectée à s qui est ensuite connecté à l’entrée a de X_1.

Les signaux internes peuvent aussi être utilisés comme sortie d’affectations continues.

Par exemple l’additionneur 1 bit aurait pu être décrit comme suit:

module FA2(
          input  logic a,
          input  logic b,
          input  logic ci,
          output logic s,
          output logic co );

   logic hs, hc;

   assign hs = a ^ b;
   assign hc = a & b;

   assign s = hs ^ ci;
   assign co = hc |  hs & ci;

endmodule

Ceci est utile pour structurer son code et le rendre plus lisible.

Avec ce complément de syntaxe, nous pouvons décrire la structure de l’additionneur 4 bits.

Notez aussi qu’il n’y a pas besoin d’importer de bibliothèque ou d’inclure de fichiers d’en-tête en SystemVerilog. Il suffit que l’outil voit les différents modules.

Pour DigitalJS, il suffit que les différents modules soient présents dans le même fichier ou dans des fichiers (onglets) différents.

Travail à faire Tester dans DigitalJS et vérifiez que le comportement est correct.

Complément: Comment décrire le comportement de l’additionneur (et non sa structure)

Habituellement, pour décrire un opérateur aussi commun qu’un aditionneur, on utilise les opérateurs arithmétiques de SystemVerilog pour décrire le comportement (plutôt que la structure). La décomposition en des opérateurs en portes élémentaire étant faite par l’outil informatique qui analyse le code (on parle d’outil de synthèse).

La seule difficulté ici étant de récupérer la retenue sortante. Pour cela, il suffit de faire l’addition sur un bit de plus en déclarant un signal interne, comme montré dans l’exemple suivant.

module ADDER4(
          input  logic [3:0] a,
          input  logic [3:0] b,
          input  logic ci,
          output logic [3:0] s,
          output logic co );

   logic[4:0] s_i;

   assign s_i = a + b + ci;
   assign s = s_i[3:0];
   assign co = s_i[4];

endmodule

En SystemVerilog il existe un opérateur de concaténation qui permet de regrouper des éléments pour construire des vecteurs/bus. Pour cela on utilise les accolades { et }.

Par exemple:

logic a, b;
logic [1:0] c,d;

// {a,b} vecteur de 2 bits avec a en msb
assign d = {a,b};
// légal à droite et à gauche d'une affectation
assign {a,b} = c;

Ceci permet de simplifier l’écriture de l’additionneur en se passant du signal intermédiaire.

Pour illustrer cela, nous allons prendre comme exemple le code décrivant un multiplexeur 2 vers 1.

Nous savons retranscrire, en SystemVerilog, l’équation logique d’un multiplexeur. Ceci permet de décrire le comportement de cette porte sans avoir à le décrire structurellement comme une combinaison de portes ET et OU.

Malgré cela, cette description reste assez bas niveau puisqu’on doit malgré tout connaitre l’équation booléenne.

En SystemVerilog, l’opérateur ternaire peut être utilisé pour exprimer ce comportement. En fonction de la valeur de s on obtient la valeur venant de a ou b.

Cette description du même multiplexeur est un peu plus abstraite, on exprime le comportement de la porte sans devoir expliciter son équation booléenne.

Attention ceci reste la description d’un composant électronique et non une instruction qui s’exécute. On compte sur les outils utilisés pour interpréter ce comportement et régénérer l’équation booléenne et la structure de portes logiques.

Cette écriture a l’avantage de permettre de décrire simplement un multiplexeur de bus. Nous n’avons plus besoin d’exprimer l’équation booléenne pour chaque bit!

Par exemple, pour multiplexer des bus de 4 bits, nous pouvons juste écrire:

module MUX21x4 ( input  logic [3:0] a, b,
                 input  logic s,
                 output logic [3:0]  o    );

assign o = s? a : b;

endmodule

Il serait intéressant de monter en abstraction et décrire ce comportement avec des constructions plus haut niveau, plus simple à lire, comprendre et faire évoluer.

Le comportement du multiplexeur pourrait être exprimé par une structure explicite if...else. Pour cela, SystemVerilog ajoute la notion de processus que nous présentons dans la suite.

Les processus permettent d’utiliser des constructions plus haut niveau pour décrire de la logique.

Ici, pour décrire la logique combinatoire, on voit apparaitre le bloc précédé par le mot clé always_comb. Ce bloc est délimité par les mots clés begin et end (qui remplacent les accolades { et } qu’on aurait en langage C ou Java et qui sont utilisées en SystemVerilog pour la concaténation)

Ce bloc est appelé processus.

Dans l’exemple précédent, ce processus décrit le comportement du même multiplexeur. Toujours à la charge de l’outil d’analyser ce comportement et de le remplacer par la structure de porte adéquate.

Note Comment l’interpréter et pourquoi always_comb?

• C’est un composant matériel, donc, tout le temps (always),
  • si l’une de se entrées change (dans l’exemple a,b ou s),
  • on relance ce fragment de code pour réévaluer (ou calculer) la valeur de la sortie o

C’est l’exécution de ce fragment de code qui décrit le comportement du bloc combinatoire. On doit garantir que le comportement décrit correctement de la logique combinatoire et que la valeur de la sortie est définie pour toutes les valeurs possibles des entrées à chaque fois que le processus est évalué.

Ce dernier point est important, et pour l’exemple du multiplexeur, ceci veut dire que la valeur de la sortie doit être définie pour les deux branches du if.

En plus de la structure if...else, une construction case existe SystemVerilog. Elle permet d’énumérer les différents cas.

Notez que la syntaxe est différente de celle du C et qu’elle se termine par le mot clé endcase.

Comme pour la structure if...else la valeur de la sortie doit être définie pour toutes les valeurs possibles des entrées.

Avec cette nouvelle structure, nous pouvons décrire de façon compacte des comportements ou le nombre de cas est plus grand que deux.

Par exemple, voici la description d’un multiplexeur 4 \rightarrow 1 de bus de 4  bits:

module MUX41x4 ( input  logic [3:0] a, b, c, d,
                 input  logic [1:0] s,
                 output logic [3:0]  o    );
always_comb
begin
   case(s)
      0: o = a;
      1: o = b;
      2: o = c;
      3: o = d;
   endcase
end
endmodule

Comme l’entrée de sélection s est sur 2 bits, il y a 4 cas à décrire.

Attention le nombre de cas sera toujours une puissance de 2 (2^n ou n est la taille du signal testé). Si tous les cas ne sont pas utilisés, il faudra malgré tout donner une valeur à la sortie pour ces cas (sinon ce n’est pas de la logique combinatoire).

Pour cela, le langage prévoit un cas par défaut comme le montre l’exemple suivant:

module MUX31x4 ( input  logic [3:0] a, b, c,
                 input  logic [1:0] s,
                 output logic [3:0]  o    );
always_comb
begin
   case(s)
      0: o = a;
      1: o = b;
      default: o = c; // si s == 2 ou 3
   endcase
end
endmodule

En SystemVerilog, en plus de la base, on peut exprimer explicitement la taille (nombre de bit) sur lequel un nombre est représenté.

Un nombre se représente sous la forme N'Bxxxx où N est la taille en bits et B la base dans laquelle il est représenté (d pour décimal, b pour binaire et h pour hexadécimal).

Important

• Si la base n’est pas précisée, le nombre est décimal sur 32 bits.
• On ne peut pas préciser la taille sans préciser la base.
• Pour la lisibilité on peut séparer les chiffres par _

Exemples:

Nous désirons écrire le code SystemVerilog d’un décodeur combinatoire pour contrôler un afficheur 7 segments. Chaque segment est en réalité une LED, dont on contrôle la cathode.

• on l’allume en la mettant 0
• on l’éteint en la mettant 1

Les 7 segments permettent d’afficher, en hexadécimal, toutes les valeurs d’un nombre entre 0 et 15. En plus, de ces 7 segments, notre afficheur contient un point que l’on peut contrôler de façon similaire.

Complétez, puis testez (en utilisant DigitalJS) le module suivant:

1. Écrire la table de vérité permettant de contrôler l’état des 7 segments en fonction de la valeur de num.
2. Écrire le code de ce décodeur combinatoire utilisant un processus et la construction case.
3. Ajouter le nécessaire pour gérer le point.

Notes les indices des bits de la sortie display7 correspondent aux numéros sur la figure. Le point correspond au bit de poids fort (numéro 7) de la même sortie. L’entrée sur 4 bits num correspond à la valeur à décoder, l’entrée dot à une commande séparée pour le point.

Magie de la simulation, DigitalJS vous affichera un afficheur, tant que la sortie s’appelle display7.